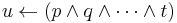Horn clause

In mathematical logic, a Horn clause is a clause (a disjunction of literals) with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951. Horn clauses play a basic role in logic programming and are important for constructive logic.

A Horn clause with exactly one positive literal is a definite clause; in universal algebra definite clauses appear as quasiidentities. The positive literal is called the head and the negative literals form the body of the clause. A Horn clause containing only negative literals is sometimes called a goal clause or query clause, especially in logic programming. A dual-Horn clause is a clause with at most one negative literal. A definite clause with no negative literals simply asserts a given propostion sometimes called a fact. A Horn formula is a string of existential or universal quantifiers followed by a conjunction of Horn clauses; that is, a prenex normal form formula whose matrix is in conjunctive normal form with all Horn clauses.

The following is an example of a (definite) Horn clause:

$\neg p \or \neg q \vee \cdots \vee \neg t \vee u$

Such a formula can also be written equivalently in the form of an implication:

$(p \wedge q \wedge \cdots \wedge t) \rightarrow u$

Horn clauses can be propositional or first order, depending on whether we consider propositional or first-order literals.

Horn (1951) has shown that validity of Horn formulas is preserved under nonempty direct products, and conjectured that the converse also holds. This was disproved by Chang and Morel (1958), however Keisler (1965) proved that a formula is Horn if and only if it is preserved under nonempty reduced products.

Horn clauses are relevant to theorem proving by first-order resolution, in that the resolution of two Horn clauses is itself a Horn clause. Moreover, the resolution of a goal clause and a definite clause is again a goal clause. In automated theorem proving, this can lead to greater efficiencies in proving a theorem represented as a goal clause.

Horn clause logic is equivalent in computational power to a universal Turing machine. In fact, the resolution of a goal clause with a definite clause to produce a new goal clause is the basis of the SLD resolution inference rule, used to implement logic programming and the programming language Prolog. In logic programming a definite clause behaves as a goal-reduction procedure. For example, the Horn clause written above behaves as the procedure:

to show $u$ , show $p$ and show $q$ and $\cdots$ and show $t$ .

To emphasize this backwards use of the clause, it is often written using the consequence operator:

$u \leftarrow (p \and q \and \cdots \and t)$

This is written in Prolog as follows:

u :- p, q, ..., t.

Propositional Horn clauses are also of interest in computational complexity, where the problem of finding a set of variable assignments to make a conjunction of Horn clauses true is a P-complete problem (in fact solvable in linear time), sometimes called HORNSAT.^[1] (The unrestricted Boolean satisfiability problem is an NP-complete problem however.) Satisfiability of first-order Horn clauses is undecidable.

References

^ Stephen Cook; Phuong Nguyen (2010). Logical foundations of proof complexity. Cambridge University Press. p. 224. ISBN 9780521517294. http://books.google.com/books?id=2aW2sSlQj_QC&pg=PA224.

Alfred Horn (1951), "On sentences which are true of direct unions of algebras", Journal of Symbolic Logic, 16, 14–21.
C. C. Chang, A. C. Morel (1958), "On closure under direct product", Journal of Symbolic Logic, 23, 149–154.
H. J. Keisler (1965), "Reduced products and Horn classes", Transactions of the American Mathematical Society, 117, 307–328.
Dowling, W., and Gallier, J. (1984), "Linear-time algorithms for testing the satisfiability of propositional Horn formulae". Journal of Logic Programming, 3, 267-284

External links

Alex Sakharov, "Horn Clause" from MathWorld.

This article was originally based on material from the Free On-line Dictionary of Computing, which is licensed under the GFDL.